By Kevin Speyer
Table of Contents
Reinforcement Learning (RL) has gained a lot of attention due to its ability to surpass humans at numerous table games like chess, checkers and Go. If you are interested in AI, you have surely seen the video where a RL trained program finishes a Supermario level.
In this post, I'll show you how to write your first RL program from scratch. Then, I'll show how this algorithm manages to find better solutions for the Travelling Salesman Problem (TSP) than Google’s specialised algorithms. I will not go through the mathematical details of RL. You can read an introduction of Reinforcement Learning in this article and also in this article.
We will use a model-free RL named Q-learning. The key element in this algorithm is Q(s,a), which gives a score for each action (a) to take, given the state (s) that the agent is in. During training, the agent will go through various states and estimate what the total reward for each possible action is, taking into account the short- and long-term consequences. Mathematically speaking, this is written:
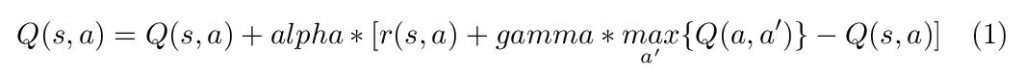
The parameters are alpha (learning rate) and gamma (discount factor). r(s,a) is the immediate reward for taking actions a under state s. The second term, max_a' ( Q(a,a') ), is the tricky one. This adds the future reward to Q(s,a) so that long-term objectives are taken into account in Q(s,a). Gamma is a discount factor between 0 and 1 that gives a lower weight to distant events in the future.
Now it's just a matter of mapping states, rewards and actions to a specific problem. We will solve the Travelling Salesman Problem using Q-learning. Given a set of travelling distances between destinations, the problem is to find the shortest route to visit every location. In this case, we will start and finish in the same location, so it's a round trip. Now we need to map the problem to the algorithm.
Naturally, the state s is the location the salesman is at. The possible actions are the points he can visit; that was easy! Now, what is the immediate reward for going from point 0 to point 1? We want the reward to be a monotonic descendent function with respect to travelling distance. That is: less distance, more reward. In this case I used r(s,a) = 1/d_sa, where d_sa is the travelling distance between point s and point a. We are assuming that there is no 0 distance travel between points. Another possibility is to use r(s,a)=-d_sa.
First, we have to obtain the data. In this case, the given data is the location of each city to be visited by the salesman. Typically, this kind of data is stored in databases (DB). This means that we have to connect and query the DB to extract the relevant information. In this case I used PostgreSQL due to its features and simplicity. The programming language of choice for this project is python, because it is the most popular option for data science projects.
Let’s set the connection to the DB:
|
1 2 3 |
import psycopg2 connection = psycopg2.connect(user = 'usname', database = 'db_name') cursor = connection.cursor() |
In usname and db_name you should write your username and database name, respectively. Now we have to query the DB, and get the position of each city:
|
1 2 |
cursor.execute("select x_coor, y_coor from city_locations;") locations = cursor.fetchall() |
Finally, we have to calculate the distances between each pair of cities and save it as a matrix:
|
1 2 3 4 5 6 7 |
import numpy as np n_dest = len(locations) # 20 destinations in this case dist_mat = np.zeros([n_dest,n_dest]) for i,(x1,y1) in enumerate(locations): for j,(x2,y2) in enumerate(locations): d = np.sqrt((x1-x2)**2+(y1-y2)**2) # Euclid distance dist_mat[i,j] = d |
We will define just one function which will be responsible for updating the elements of the Q-matrix in the training phase according to equation 1.
|
1 2 3 4 5 |
def update_q(q, dist_mat, state, action, alpha=0.012, gamma=0.4): immed_reward = 1./ dist_mat[state,action] # Set immediate reward as inverse of distance delayed_reward = q[action,:].max() q[state,action] += alpha * (immed_reward + gamma * delayed_reward - q[state,action]) return q |
Now we can train the RL model by letting the agent run through all the destinations, collecting the rewards. We will use 2000 training iterations.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
q = np.zeros([n_dest,n_dest]) epsilon = 1. # Exploration parameter n_train = 2000 # Number of training iterations for i in range(n_train): traj = [0] # initial state is the warehouse state = 0 possible_actions = [ dest for dest in range(n_dest) if dest not in traj] while possible_actions: # until all destinations are visited #decide next action: if random.random() < epsilon: # explore random actions action = random.choice(possible_actions) else: # exploit known data from Q matrix best_action_index = q[state, possible_actions].argmax() action = possible_actions[best_action_index] # update Q: core of the training phase q = update_q(q, dist_mat, state, action) traj.append(action) state = traj[-1] possible_actions = [ dest for dest in range(n_dest) if dest not in traj] # Last trip: from last destination to warehouse action = 0 q = update_q(q, dist_mat, state, action) traj.append(0) epsilon = 1. - i * 1/n_train |
The parameter epsilon (between 0 and 1) controls the exploration vs exploitation ratio in training. If epsilon is near 1, then the agent will take random decisions and explore new possibilities. A low value of epsilon means the agent will take the best known path, exploiting the information already acquired. A well-known policy is to lower this epsilon parameter as the model gains insight into the problem. At the beginning, the agent takes random actions and explores different routes, and as the Q matrix gains more useful information, the agent is more likely to take the path of greater reward.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
traj = [0] state = 0 distance_travel = 0. possible_actions = [ dest for dest in range(n_dest) if dest not in traj ] while possible_actions: # until all destinations are visited best_action_index = q[state, possible_actions].argmax() action = possible_actions[best_action_index] distance_travel += dist_mat[state, action] traj.append(action) state = traj[-1] possible_actions = [ dest for dest in range(n_dest) if dest not in traj ] # Back to warehouse action = 0 distance_travel += dist_mat[state, action] traj.append(action) #Print Results: print('Best trajectory found:') print(' -> '.join([str(b) for b in traj])) print(f'Distance Travelled: {distance_travel}') |
The agent starts at the warehouse and runs through all cities according to the Q matrix, trying to minimise the total distance of the route.
To compare the solutions given by this algorithm, we will use the QR-tools TSP solver from Google. This is a highly specialised algorithm particularly designed to solve the TSP, and has great performance. After playing around with the RL algorithm and tuning the parameters (alpha and gamma), I was surprised to see that our RL algorithm was able to find shorter routes than Google's algorithm in some cases.
|
1 2 |
RL route: 0 -> 7 -> 17 -> 2 -> 19 -> 4 -> 8 -> 9 -> 18 -> 14 -> 11 -> 3 -> 6 -> 12 -> 10 -> 16 -> 13-> 1 -> 5 -> 15 -> 0; distance: 3511 Google route 0 -> 7 -> 17 -> 2 -> 19 -> 4 -> 8 -> 9 -> 18 -> 14 -> 11 -> 3 -> 6 -> 5 -> 10 -> 16 -> 13-> 1 -> 12 -> 15 -> 0; distance: 3767 |
The Reinforcement Learning algorithm was able to beat the highly specific algorithm by almost 7%! It is worth mentioning that most of the time, OR-Tools’ algorithm finds the best solution, but not infrequently, our simple RL algorithm finds a better solution.
+43 (0) 2622 93022-0
office@cybertec.at
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information