Pgbench is a very well-known and handy built-in tool that Postgres DBAs can use for quick performance benchmarking. Its main functionality/flow is super simple, but it also has some great optional features, like running custom scripts and specifying different probabilities for them. One can also use bash commands to fill query variables for example.
Table of Contents
But the thing that has always annoyed me a bit, is the fact that one cannot specify the desired database or table size but has to think in so called "scaling factor" numbers. And we know from documentation, that scaling factor of "1" means 100k rows in the main data table "pgbench_accounts". But how the does scaling factor of 100 (i.e. 10 Million bank accounts) translate to disk size? Which factor do I need to input when wanting to quickly generate a database of 50 GB to see how random updates would perform, in case the dataset does not fit into RAM/shared buffers. Currently there is a bit of trial and error involved 🙁 So how to get rid of the guesswork and be a bit more deterministic? Well I guess one needs a formula that translates input of DB size to scaling factor!
One way to arrive at the magic formula would be to generate a lot of sample data for various scaling factors, measure the resulting on-disk sizes and deriving a formula out of it. That's exactly what I've done.
So I hatched up the script below and booted up a GCE instance, destined to churn the disks nonstop for a bit more than a whole day as it appeared - I'm sorry little computer 🙂 The script is very simple - it runs the pgbench schema initialization with different scaling factors from 1 to 50k and stores the resulting DB/table/index sizes in a table, so that later some statistics/maths could be applied to infer a formula. NB! Postgres version used was 10.1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
psql -c 'create table if not exists init_results (scale int not null, table_size_mb int not null, index_size_mb int not null, db_size_mb int not null);' SCALES='1 10 50 100 150 200 250 300 350 400 450 500 750 1000 1500 2000 2500 3000 3500 4000 4500 5000 6000 7000 8000 9000 10000 12500 15000 17500 19999 20000 25000 30000 35000 40000 45000 50000' for x in $SCALES ; do pgbench -i --unlogged-tables -s $x -n &>/tmp/pgbench.log SQL=$(cat <<-EOF insert into init_results select ${x}, (select round(pg_table_size('pgbench_accounts') / 1024^2)), (select round(pg_relation_size('pgbench_accounts_pkey') / 1024^2)), (select round(pg_database_size(current_database()) / 1024^2)) EOF ) echo '$SQL' | psql done |
After the script finished (25h later...note that without the "--unlogged-tables" flag it would take a lot longer), I had a nice table showing how different scaling factors translate to database size on disk, measured in MB (MiB/mebibytes to be exact, i.e. 1MB=1048576 bytes) as this is what the "psql" client is using when reporting object sizes.
So now how to turn this data around so that we get a formula to calculate scaling factors, based on input target DB size? Well I'm sure there are quite some ways and countless Statistics/Data Mining techniques could be applied, but as Data Science is not my strongest skill I thought I'll first take the simplest possible road of using built in statistics functions of a spreadsheet program and see how it fares. If the estimation doesn't look good I could look for something more sophisticated, scikit-learn or such. But luckily it worked out quite well!
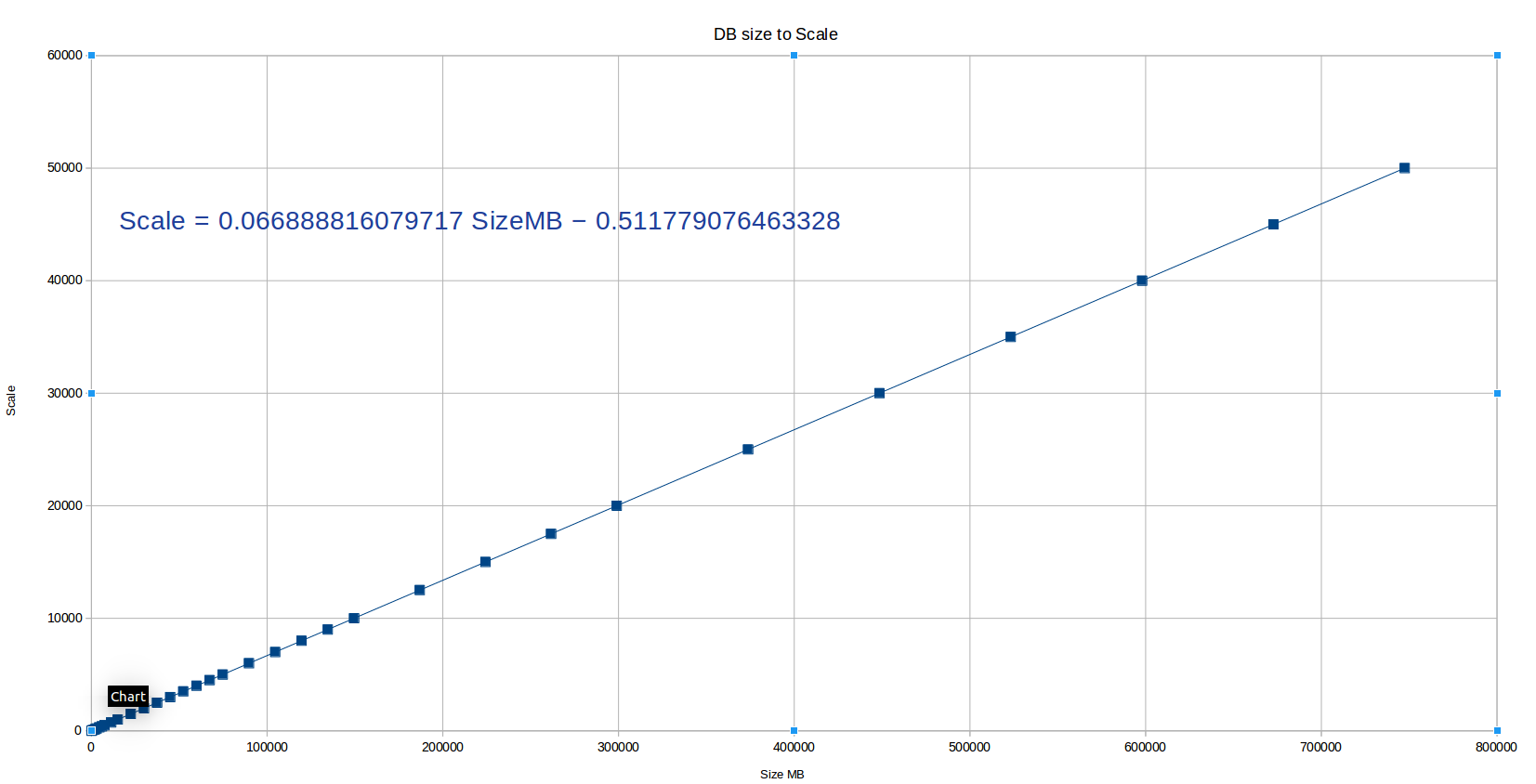
LibreOffice (my office suite of choice) is nowhere near MS Excel but it does have some quite good Statistical Regression functionalities built in and one has options to calculate regression constants together with accuracy coefficients or calculate the formulas and draw them on charts as "Trend Lines". I went the visual way. It goes something like that – create a normal chart, activate it with a double-click and then right click on some data point on the chart and select "Insert Trend Line" from the appearing popup menu. On the next screen one can choose if the "to be fitted" formula for your data should be a simple linear one or a logarithmic/exponential/polynomial. In the case of pgbench data at hand though, after trying out all of them, it appeared that there was no real extra accuracy from the more complex formulas, so I decided to apply KISS here, meaning a simple linear formula. If you look at the script you'll see that we also gathered also size data for the "pgbench_accounts" table and index data, thus for completenes,s I also generated the formulas for calculating scaling factors from target "pgbench_accounts" table/index sizes, but mostly it should not be of interest as the prominent table makes up 99% of the DB size.
So without further ado, below are the resulting formulas and a graph showing how pgbench scale changes according to DB size. I also created a small JSFiddle that you can bookmark here if you happen to work with pgbench a lot.
NB! Accuracy here is not 100% perfect of course as there are some non-linear components (pgbench_accounts.aid changes to int8 from scale 20k, index leaf density varies minimally) but it is really "good enough", meaning <1% accuracy error. Hope you find it useful and would be nice if something similar ends up in "pgbench" tool itself one day.
| Target object | Scale Formula |
|---|---|
| DB | 0.0669 * DB_Size_Target_MB - 0.5 |
| Table (pgbench_accounts) | 0.0781 * Table_Size_Target_MB |
| Index (pgbench_accounts_pkey) | 0.4668 * Index_Size_Target_MB |
+43 (0) 2622 93022-0
office@cybertec.at
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information
I keep coming back to this wonderful article whenever I have to get the pgbench scale factor right.