As CYBERTEC keeps expanding, we need a lot more office space than we previously did. Right now, we have a solution in the works: a new office building. We wanted something beautiful, so we started to dig into mathematical proportions to achieve a reasonable level of beauty. We hoped to make the building not just usable, but also to have it liked by our staff.
Table of Contents
I stumbled upon some old books about proportions in architecture and went to work. Fortunately, one can use PostgreSQL to do some of the more basic calculations needed.
This is of course a post about PostgreSQL, and not about architecture-- but let me explain a very basic concept: golden proportions. Beauty is not random; it tends to follow some mathematical rules. The same is true in music. “Golden proportions” are a common concept: Let’s take a look:
|
1 2 3 4 5 6 7 |
test=# SELECT 1.618 AS constant, round(1 / 1.618, 4) AS inverted, round(pow(1.618, 2), 4) AS squared; constant | inverted | squared ----------+----------+--------- 1.618 | 0.6180 | 2.6179 (1 row) |
We are looking at a magic number here: 1.618. It has some nice attributes. If we invert it is basically “magic number - 1”. If we square it, what we get is “magic number + 1”. If we take a line and break it up into two segments we can use 1 : 1.618. Humans will tend to find this more beautiful than splitting the line using 1 : 1.8976 or so.
Naturally we can make use of this wisdom to create a basic rectangle:
In the case of our new building, we decided to use the following size:
|
1 2 3 4 5 |
test=# SELECT 16.07, 16.07 * 1.618; ?column? | ?column? ----------+---------- 16.07 | 26.00126 (1 row) |
The basic layout is 16 x 26 meters. It matches all mathematical proportions required in the basic layout.
To make the building look more appealing, we decided to add a small semi-circle to the rectangle. The question is: What is the ideal diameter of the semi-circle? We can use the same formula as before:
|
1 2 3 4 5 6 7 |
test=# WITH semi_circle AS (SELECT 16.07 * 0.618 AS size) SELECT size, size / 2 FROM semi_circle; size | ?column? ---------+-------------------- 9.93126 | 4.9656300000000000 (1 row) |
I have used a CTE (common table expression) here. PostgreSQL 13 has a nice feature to handle those expressions. Let’s take a look at the execution plan:
|
1 2 3 4 5 6 7 |
test=# explain WITH semi_circle AS (SELECT 16.07 * 0.618 AS size) SELECT size, size / 2 FROM semi_circle; QUERY PLAN ------------------------------------------- Result (cost=0.00..0.01 rows=1 width=64) (1 row) |
The optimizer has inlined the expression. What we get is:
|
1 |
SELECT 16.07 * 0.618, SELECT 16.07 * 0.618 / 2 |
Then, the optimizer does “constant” folding. All that is left in the execution plan is a “result” node which just displays the answer. The CTE has been removed from the plan entirely.
To make sure the front of the building is not too boring, we need to figure out which numbers are “allowed” and which ones are not. The way to do that is to use recursion:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
test=# WITH RECURSIVE x AS ( SELECT 26::numeric AS base, 26*0.382::numeric AS short, 26*0.618::numeric AS long UNION ALL SELECT round((base * 0.618)::numeric, 4), round((long * 0.382)::numeric, 4), round((long * 0.618)::numeric, 4) FROM x WHERE base > 0.5 ) SELECT * FROM x WHERE base > 0.5; base | short | long ---------+--------+-------- 26 | 9.932 | 16.068 16.0680 | 6.1380 | 9.9300 9.9300 | 3.7933 | 6.1367 6.1367 | 2.3442 | 3.7925 3.7925 | 1.4487 | 2.3438 2.3438 | 0.8953 | 1.4485 1.4485 | 0.5533 | 0.8952 0.8952 | 0.3420 | 0.5532 0.5532 | 0.2113 | 0.3419 (9 rows) |
The idea is to make sure that all components are related to all other components. What we do here is start with 26 meters and calculate the “long” and the “short sides”. Then we use this input for the next iteration, so that we can get a series of valid numbers which guarantee that things fit perfectly. Fortunately, PostgreSQL can do recursion in a nice, ANSI-compatible way. Inside the WITH the first SELECT will assign the start values of the recursion. Then the second part after the UNION ALL will call the recursion which is terminated by the WHERE-clause. At the end of the day, we get a sequence of mathematically correct numbers.
However, once in a while you want to see which iteration a line belongs to. Here is how this can be achieved:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
test=# WITH RECURSIVE x AS ( SELECT 26::numeric AS base, 26*0.382::numeric AS short, 26*0.618::numeric AS long UNION ALL SELECT round((base * 0.618)::numeric, 4), round((long * 0.382)::numeric, 4), round((long * 0.618)::numeric, 4) FROM x WHERE base > 0.5 ) SELECT row_number() OVER (), * FROM x WHERE base > 0.5; row_number | base | short | long ------------+---------+--------+-------- 1 | 26 | 9.932 | 16.068 2 | 16.0680 | 6.1380 | 9.9300 3 | 9.9300 | 3.7933 | 6.1367 4 | 6.1367 | 2.3442 | 3.7925 5 | 3.7925 | 1.4487 | 2.3438 6 | 2.3438 | 0.8953 | 1.4485 7 | 1.4485 | 0.5533 | 0.8952 8 | 0.8952 | 0.3420 | 0.5532 9 | 0.5532 | 0.2113 | 0.3419 (9 rows) |
row_number() is a function returning a simple number indicating the line we are looking at.
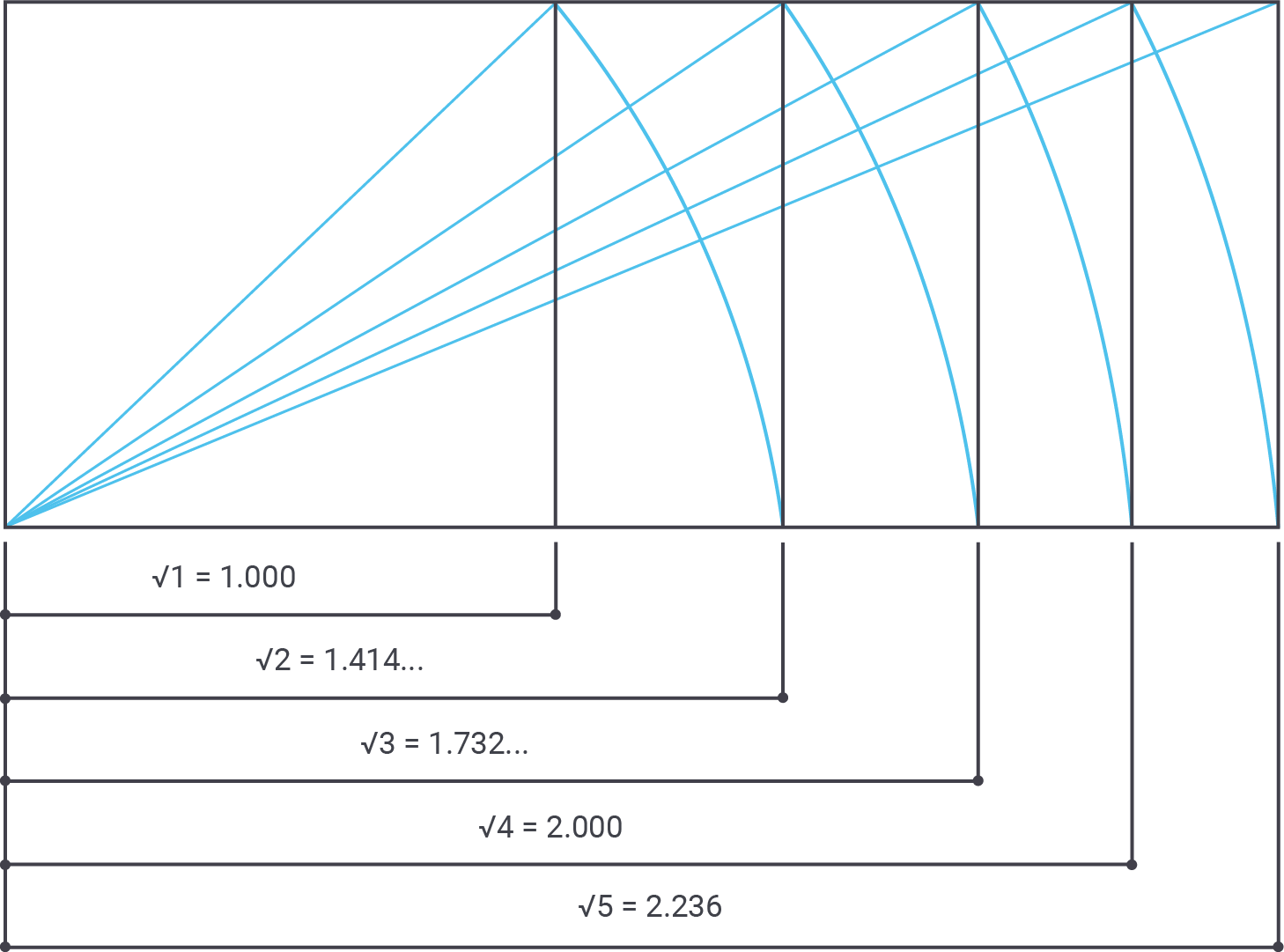
However, there are more “good” numbers in architecture than golden proportions. Square roots and so on are also important. To help calculate those numbers one can use a function:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
BEGIN; CREATE TYPE good_number_type AS ( base numeric, golden_short numeric, golden_long numeric, sqrt2 numeric, sqrt3 numeric, sqrt4 numeric, sqrt5 numeric ); CREATE OR REPLACE FUNCTION good_numbers(numeric) RETURNS good_number_type AS $ SELECT ($1, 0.382 * $1, 0.618 * $1, sqrt(2) * $1, sqrt(3) * $1, 2 * $1, sqrt(5) * $1 )::good_number_type; $ LANGUAGE 'sql'; COMMIT; |
Golden proportions are a good thing. However, sometimes it is not possible to use those numbers alone. If we look at some of the greatest buildings (Pantheon, etc.) in the world, we will see that the architects also worked with square roots, cubic roots and so on.
The way to do that in PostgreSQL is to use a function. However, in this case we want a function to return more than just one field. The solution to the problem is a composite data type. It can return more than just one value.
|
1 2 3 4 5 6 7 8 9 10 11 |
test=# x Expanded display is on. test=# SELECT * FROM good_numbers(16); -[ RECORD 1 ]+----------------- base | 16 golden_short | 6.112 golden_long | 9.888 sqrt2 | 22.6274169979695 sqrt3 | 27.712812921102 sqrt4 | 32 sqrt5 | 35.7770876399966 |
22, 27m, and 35m meters are obviously correct values which we can use to ensure beauty.
What you see is that we have used the function call for one number. However, sometimes you might want to calculate things for many values. To do that, it is important to understand how you can handle the return value of composite types:
|
1 2 3 4 |
test=# SELECT a FROM good_numbers(16) AS a; -[ RECORD 1 ] ------------------------------------------------------------ a | (16,6.112,9.888,22.6274169979695,27.712812921102,32,35.7770876399966) |
As you can see, “a” can be used in the SELECT-clause (“target list”) directly. The result is not that readily readable-- however, it is possible to expand this field and extract individual columns as shown in the next listing:
|
1 2 3 4 5 6 |
test=# SELECT (a).base, (a).golden_short, (a).golden_long FROM good_numbers(16) AS a; base | golden_short | golden_long ------+--------------+------------- 16 | 6.112 | 9.888 (1 row) |
This opens the door to calculate our numbers for an entire series of numbers:
|
1 2 3 4 5 6 7 8 9 |
test=# SELECT (good_numbers(id)).* FROM generate_series(1, 4) AS id; base | golden_short | golden_long | sqrt2 | sqrt3 | sqrt4 | sqrt5 ------+--------------+-------------+------------------+------------------+-------+------------------ 1 | 0.382 | 0.618 | 1.4142135623731 | 1.73205080756888 | 2 | 2.23606797749979 2 | 0.764 | 1.236 | 2.82842712474619 | 3.46410161513775 | 4 | 4.47213595499958 3 | 1.146 | 1.854 | 4.24264068711929 | 5.19615242270663 | 6 | 6.70820393249937 4 | 1.528 | 2.472 | 5.65685424949238 | 6.92820323027551 | 8 | 8.94427190999916 (4 rows) |
All we did was to pass the “id” to the function and expand those columns.
If you want to learn more about upgrading PostgreSQL, you should check out our blog post about logical replication.
Leave a Reply