Last time, we experimented with lesser known PostGIS functions to extract areas of interest for sales. Now, let’s extend our example regarding catchment areas by optimizing trips within the area of interest we generated in our previous example, which is around Hamburg. Let’s ask the following question:
which order should we visit our major cities in so that we can optimize our trip’s costs?
Table of Contents
This optimization problem is commonly known as the Traveling Salesman Problem (or TSP).
Apart from PostGIS, pgRouting will be used to tackle this challenge within PostgreSQL only. pgRouting is served as a PostgreSQL extension, which adds a lot of geospatial routing functionality on top of PostGIS.
I recommend you check out its online documentation, located at https://pgrouting.org/, to get an overview.
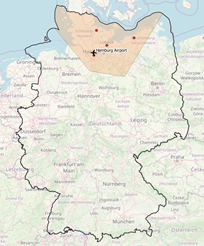 | 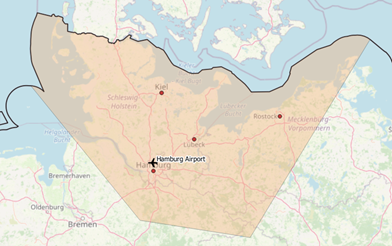 |
Figure 1 Area of interest around Hamburg / Figure 2 Area of interest around Hamburg, Zoom
This article is organized as follows:
We will re-use osm files and datasets processed in my last blogpost, so first, please play through the blogpost sections involved. Subsequently, an intermediate table “tspPoints” must be created, which contains major cities and airports covered by our preferred area around Hamburg only (see the annex for ddl).
To solve TSP by utilizing our pgRouting functionality, we must generate a graph out of osm data. Different tools like osm2pgrouting or osm2po exist, which generate a routable graph from plain osm data. Due to limited memory resources on my development machine, I decided to give osm2po a try.
So then - let’s start. After downloading the latest osm2po release from https://osm2po.de/releases/,
we need to adapt its configuration, in order to generate the desired graph as an sql file.
Please uncomment the following line in osm2po.config to accomplish this task.
postp.0.class = de.cm.osm2po.plugins.postp.PgRoutingWriter
Now we’re ready to generate our graph by executing
|
1 2 |
java -Xmx8g -jar osm2po-core-x.x.x-signed.jar workDir=/data/de-graph prefix=de tileSize=x /data/germany-latest.osm.pbf |
The outputted sql file can easily be imported to PostGIS by calling
|
1 |
psql -U username -d dbname -q -f /data/de-graph/de_2po_4pgr.sql |
the resulting graph table contains geometries for edges only (see annex for ddl). To generate source and target nodes too, let’s utilize pgr_createverticestable as follows:
|
1 2 |
select pgr_createverticestable('de_2po_4pgr', 'geom_way', 'source', 'target'); |
Slowly, we’re getting closer ????. Figure 3 to 5 represent our stacked layer setup on top of OpenStreetMap, which is based upon the following tables:
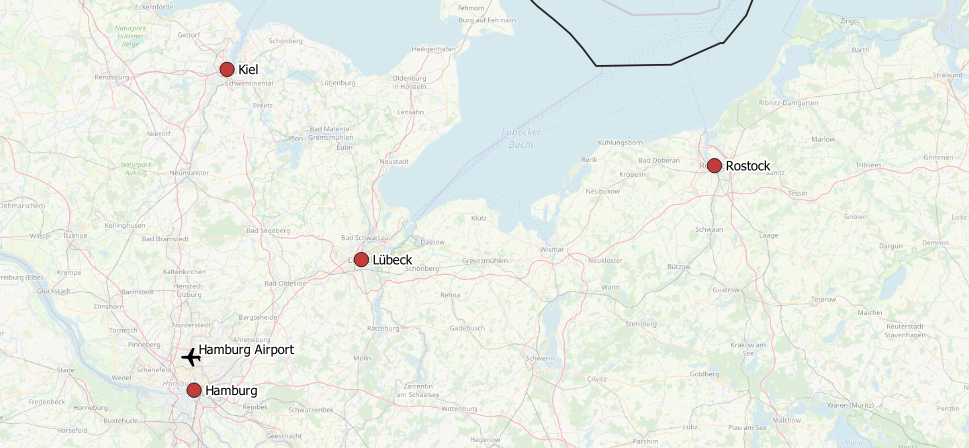 Figure 3 Intermediate trip stops | |
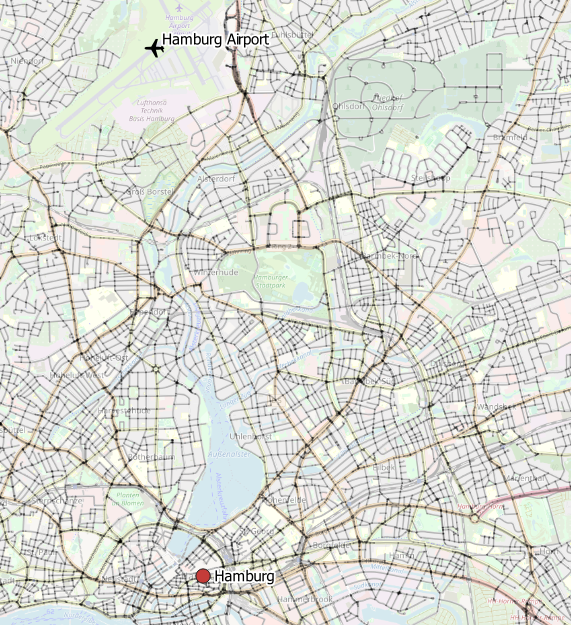 Figure 4 Edges around Hamburg | 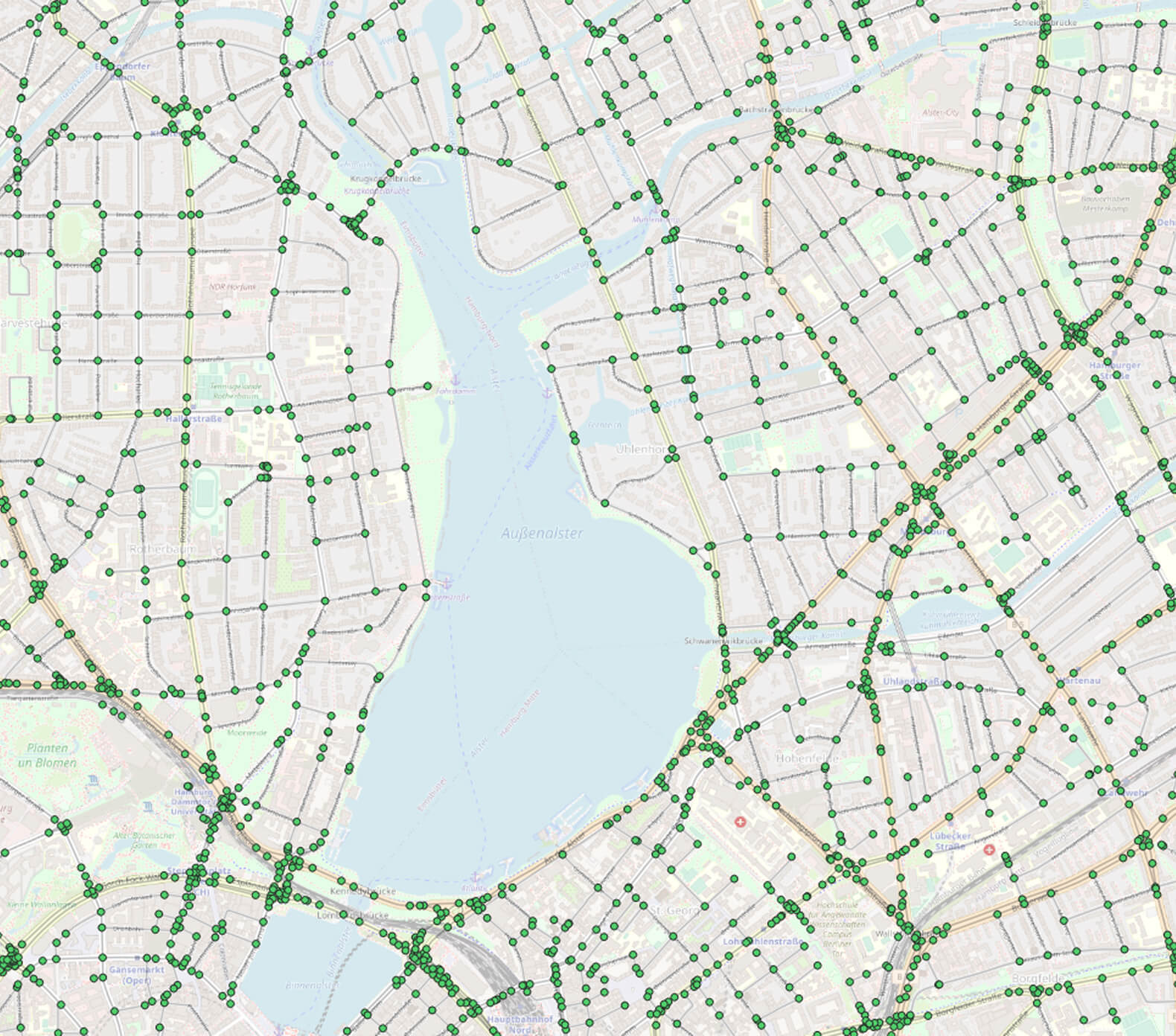 Figure 5 Edges + nodes around Hamburg |
Now let’s ask pgRouting to solve our traveling salesmen problem by querying
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
SELECT seq,node, cost, agg_cost FROM pgr_TSP( $$ SELECT * FROM pgr_dijkstraCostMatrix( 'SELECT id, source, target, cost, reverse_cost FROM de_2po_4pgr', (with nearestVertices as( SELECT a.id from tsppoints, lateral ( select id,the_geom from osmtile_germany.de_2po_4pgr_vertices_pgr order by osmtile_germany.de_2po_4pgr_vertices_pgr.the_geom <-> osmtile_germany.tsppoints.geom limit 1 ) a) select array_agg(id) from nearestVertices), directed := false) $$, start_id := 591341); |
This command results in the optimal order of intermediate stops (edges next to our cities) forming our trip. It’s worth pointing out that the optimal route (order) depends on the cost-matrix’s respective cost-function, which was defined to calculate the edge’s weights. In our case, the cost function is prescribed by osm2po and expressed as length/kmh.
To export the sequence of city names to pass through, the nodes returned by pgr_TSP must be joined back to tspPoints. Please consult the annex for this particular query extension. From figure 6 we now realize that the optimal route goes from Hamburg Airport to Kiel, Lübeck, Rostock and Hamburg before bringing us back to our airport.
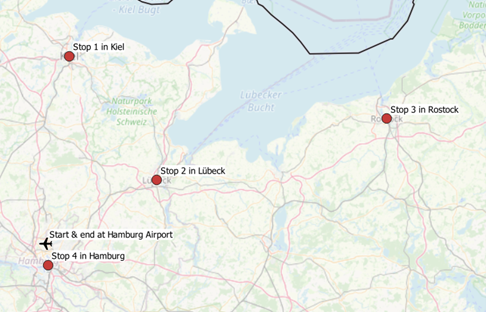
This time, we took a quick look at pgRouting to solve a basic traveling salesman problem within PostGIS. Feel free to experiment with further cost functions and to move on to calculating detailed routes between cities by utilizing further pgRouting functions.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
create table if not exists osmtile_germany.de_2po_4pgr ( id integer not null constraint pkey_de_2po_4pgr primary key, osm_id bigint, osm_name varchar, osm_meta varchar, osm_source_id bigint, osm_target_id bigint, clazz integer, flags integer, source integer, target integer, km double precision, kmh integer, cost double precision, reverse_cost double precision, x1 double precision, y1 double precision, x2 double precision, y2 double precision, geom_way geometry(LineString,4326) ); create index if not exists idx_de_2po_4pgr_source on osmtile_germany.de_2po_4pgr (source); create index if not exists idx_de_2po_4pgr_target on osmtile_germany.de_2po_4pgr (target); create index if not exists idx_de_2po_geom on osmtile_germany.de_2po_4pgr using gist (geom_way); |
|
1 2 3 4 5 6 7 8 |
create table osmtile_germany.tspPoints ( id serial primary key, name text, geom geometry(Point, 4326) ); create index idx_tspPoints on osmtile_germany.tspPoints using gist (geom); |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
SELECT seq, node, a.name, a.geom FROM pgr_TSP( $ SELECT * FROM pgr_dijkstraCostMatrix( 'SELECT id, source, target, cost, reverse_cost FROM de_2po_4pgr', ( with nearestVertices as( SELECT a.id from tsppoints, lateral ( select id, the_geom from osmtile_germany.de_2po_4pgr_vertices_pgr order by osmtile_germany.de_2po_4pgr_vertices_pgr.the_geom <-> osmtile_germany.tsppoints.geom limit 1 ) a ) select array_agg(id) from nearestVertices ), directed := false )$, start_id := 591341 ), de_2po_4pgr_vertices_pgr, lateral ( select name, geom from osmtile_germany.tsppoints order by osmtile_germany.tsppoints.geom <-> the_geom limit 1 ) a where node = id |
Do I need to somehow additionally process the tspPoints layer? I fully named all the tables as you have, but PGAdmin gives an error https://uploads.disquscdn.com/images/7ae15155930b085f6ee31166dfdf7931436077dc7cb0517b92807fa2e6446916.jpg
There is no need to further process tsppoints, just insert geometries representing your stops.